Written by Sue Gifford
The case for Space in the early years
Recently, the government proposed removing Shape, Space and Measures as a learning Goal for five year olds at the end of reception, and replacing it with a second Goal about number. Early years teachers I spoke to were adamant about the importance of SS&M for early maths. They were also convinced that, if these areas were not going to contribute to school scores of ‘Good Level of Development’, senior managers, and therefore teachers, would soon cease to focus on them in terms of time and resources.

Although some early years and primary maths colleagues argued with DfE about this proposal, it went ahead for piloting. So I set about looking at research evidence about Shape, Space and Measures education with four and five year olds. Whereas it seems there has not been much focus recently on shape and measures, I quickly found that ‘spatial reasoning ‘with young children is an active field. Two recent research sources are the Erikson Early Mathematics Collaborative and a special issue of ZDM: The International Journal on Mathematics Education (Sinclair & Bruce, 2015).
Basically, strong links have been established between young children’s spatial skills, such as visualization, and their later mathematics achievement, particularly number understanding. More importantly, it seems that spatial thinking can be taught, and is linked to play with, for instance, building blocks and jigsaw puzzles. Since some groups, such as girls and poorer children, are found to have less of this kind of experience than others, it becomes a social justice issue to provide it for all children in pre-school. As it also seems that the complexity of children’s block and puzzle play is significant, then a Goal might also support teachers’ focus on the quality of play. This would be a radical departure from the current Goal’s focus on describing shape and space, where the latter just involves positional language (DfE, 2017).
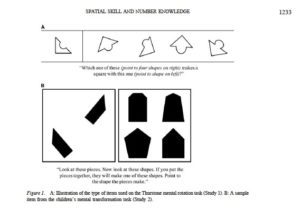
Spatial reasoning is more sophisticated than this: it involves solving problems by manipulating objects, visualizing the results of movement and interpreting images from different perspectives, including mapping your surroundings. Researchers such as Gunderson et al (2012: 1233) use tasks like these below, assessing children’s ability to predict which shapes will fit together to make another shape:
They found that results link to children’s later development of a mental number line: and the ability to place numbers on an empty number line also predicts success in calculating mentally. This suggests that developing a spatial, linear image of numbers helps children understand numerical relations. Recently, Giles et al. (2018:1335) found that primary children’s ability to hit a moving target with a bat (tested on a virtual screen) correlated with six months advance in mathematics. (This research conducted in Bradford was aptly illustrated in the Daily Telegraph– see above). Apparently, ‘interceptive timing’ eg predicting the trajectory and speed of a ball and moving your arm to meet it, involves ‘neural circuitry’ to represent time and space which overlaps with that representing number. So children who are good at spatial visualization can also form mental images of numerical relationships, which helps them to solve a range of problems. If this is so (and it must be remembered that some excellent mathematicians are hopeless ball-catchers), then developing spatial reasoning might provide some children with a route to better understanding than they have at present.
Sinclair & Bruce (2015) advocated that the geometry curriculum should move away from the current ‘passive emphasis on vocabulary (naming and sorting shapes by properties)’ and extend to ‘a more active meaning-making orientation’ including composing and decomposing shapes, comparing and mentally manipulating two- and three-dimensional figures, and mapping and orienting (2015:320). This reminded me of a comment made years ago by David Fielker, a maths educator and longtime editor of Mathematics Teaching, that it was strange that primary children operated on numbers, but only sorted and classified shapes: why didn’t they add and take away shapes too? This, of course, is what construction and shape puzzles are about. Fielker’s Starting from your head: Mental geometry (BEAM, 1993) was full of intriguing invitations to predict the result of folding and cutting shapes.
In Canada, Moss et al (2016:13) commented that spatial reasoning was ‘a curiously unacknowledged and neglected area of the curriculum’, identified by the Canadian National Research Council as a ‘blind spot’. Recent curriculum development in Canada has focused on spatial reasoning across the age range e.g. Ontario’s Paying attention to spatial reasoning K to 12.
It seems that teaching spatial reasoning would not only develop children’s ability to visualize mathematical relationships, but would provide a more active, interesting and child appropriate curriculum than some of the ‘barking names at shapes’ that currently goes on in the name of early geometry. As Freudenthal (1971:418) recommended, geometry should start “as a science of physical space, of the space in which the child lives and moves, as an organization of the learner’s spatial experiences” (cited by Sinclair and Bruce, 2015: 321).
This points to the importance of outdoor experiences generally, of children building mental maps of their surroundings through activities such as treasure hunts or obstacle courses, as well as local excursions with familiar routes. There are also interesting avenues for researchers to investigate with young children and their teachers, such as young children’s understanding of perspective and maps. Rather than omitting Shape, space and measures from the Early Learning Goals, it seems that emphasis on these should be increased, in order to provide children with increased access to and enjoyment of mathematics. It also seems that we should be encouraging more spatial reasoning and a more active approach to primary school geometry, linking to other subjects such as geography, art and computing.
Considering all this led colleagues to reflect on the current marginalization of geometry in initial teacher education, and to an informal survey of primary PGCE courses. So far it seems most students have one geometry session out of a taught maths course of under 30 hours. If you would like to contribute to this survey and receive the current results, please email the number of hours for geometry out of taught maths hours on a primary PGCE to S.Gifford@roehampton.ac.uk.
Sue Gifford
University of Roehampton, London
References:
Department for Education (2017). Statutory framework for the early years foundation stage: Setting the standards for learning, development and care for children from birth to five.
Department for Education (2018). Early years foundation stage profile 2018 handbook (pilot version September 2018).
Fielker, D. (1993). Starting from your head: mental geometry. London: BEAM.
Giles, O.T., Shire, K.A., Hill, J.B., Mushtaq, F., Waterman, A., Holt, R.J., Culmer, P.R., Williams, J.H.G., Wilkie, R.M., & Mon-Williams, M. (2018). Hitting the target: mathematical attainment in children is related to interceptive-timing ability. Psychological Science, 29(8) 1334 – doi: 10.1177/0956797618772502
Gunderson, E., Ramirez, G., Beilock, S.L. & Levine, S.C. (2012). The relation between spatial skill and early number knowledge: The role of the linear number line. Developmental Psychology, 48(5) 1229-1241. doi:10.1037/a0027433
Moss, J., Bruce, C.D., Caswell, B., Flynn, T. & Hawes, Z. (2016). Taking shape: activities to develop geometric and spatial thinking. Pearson Canada Inc., pp. 13–16.
Sinclair, N. & Bruce, C.D. (2015). New opportunities in geometry education at the primary school. ZDM Mathematics Education, 47, 319–329. doi: 10.1007/s11858-015-0693-4