More than just a game: Playing with Mathematics
Games are enjoyed by people of all ages. But can the enjoyable games become a tool to teach maths? In order to answer this question, it is helpful to analyse the relationship between expert mathematicians and games.
The memoir of Leelavati Prize winner mathematician Ali Nesin helps us to understand the special relationship between mathematicians and games. Nesin (2019), in his book “Mathematics and Fear” reveals that the most popular pastime of mathematicians at the university is playing games. He does not differentiate between games and maths as he explicitly states that “actually, it is not quite right to distinguish between math and games… In these kinds of games we play, our purpose was not to play games. Our real goal was to analyse the games, to find out the best game strategy” (p.184).
Can the games that mathematicians play be used in teaching maths in classrooms? Research and experiences show that the games are not only helpful for mathematicians but can be a part of the maths teaching process (Ernest, 1986; Pintér, 2010).
Math through Play
The contributions of games to the education of mathematics can be summarized as follows. They:
- develop participants’ problem-solving skills and motivations
- allow rich mathematical discussions
- foster mathematical reasoning
- encourage active involvement (Russo, Bragg, & Russo, 2021).
Understanding mathematics is closely related to the learner being alone with a problem and developing own solutions for this particular situation (Brousseau, 1997). Games have a great potential to create a problem situation, and they provide a suitable stimulus for the improvement of problem-solving skills. Let’s take a little game break to examine the relationship between games and the problem-solving process.
20 wins
The game ‘20 Wins’ can be a good introductory activity. It can be played by two players from any age group that can make simple additions. The rules are simple. By saying 1 or 2, the first player starts the game. 1 or 2 is added to the last number said in turn (when the first player starts the game by saying 1, the second player can say 2 or 3 etc.). The game continues in this way, until somebody reaches 20 and wins the game.
What kind of strategy do you need to develop in order to win consistently in this game?
(For those who are interested in it, I am adding the winning numbers of the game to the end of the article. Of course, you can create your own strategy before looking at the answer. Are you alone? No problem. Click to play the game online. If you want a small hint to win, it would be helpful to start at the end, a technique that is often used by mathematicians in problem solving.)
Games and problem solving
The problem solving process is widely regarded as one of the most significant aspects of doing mathematics. According to NCTM (2000, p. 52):
“Problem solving means engaging in a task for which the solution method is not known in advance. In order to find a solution, students must draw on their knowledge, and through this process, they will often develop new mathematical understandings”.
When we examine the 20 Wins game in terms of a problem solving process, it does not look like an exercise that will be solved quickly or be used a well-known method. To win consistently, you need to develop strategies by applying prior knowledge in new ways. This process will certainly involve failures but your desire to win will provide you with a great motivation to come up with new strategies. Lastly, you need to make sure that you constantly win by implementing your strategies. For this, you have to analyse game and verify your solution. Of course, the game will make you an active participant in the whole process.
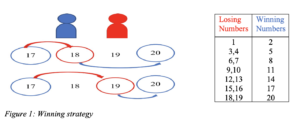
Winning strategy for 20 wins
When the last moves of the red and blue players given below are examined, it is seen that blue wins when he/she says 17. Because when 17 is said, there are two possibilities for the red player. These are 18 (by adding 1 to 17) or 19 (by adding 2 to 17). When the red player says 18 or 19, the blue player will reach 20 in both of these possibilities. When the pattern continues, the following losing and winning numbers emerges. It’s also possible to generalize the winning numbers a little more mathematically as 3n+2. Of course, don’t forget to start the game first.
References
Brousseau, G. (1997). Theory of didactical situations in mathematics: Didactique desmathématique. Kluwer Academic Publishers.
Ernest, P. (1986). Games. A rationale for their use in the teaching of mathematics in school. Mathematics in School, 15(1), 2-5. http://www.jstor.org/stable/30216298
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. Reston: NCTM
Nesin, A. (2019). Matematik ve korku (Math and fear). Nesin Yayıncılık.
Pintér, K. (2010). Creating games from mathematical problems. Primus, 21(1), 73-90. https://doi.org/10.1080/10511970902889919
Russo, J., Bragg, L. A., & Russo, T. (2021). How primary teachers use games to support their teaching of mathematics. International Electronic Journal of Elementary Education, 13(4), 407-419.
Yasin Memis taught mathematics at the middle schools for about 10 years. He is currently a PhD student in mathematics education at Anadolu University (Turkey). His research is mainly focused on curriculum and task design. Yasin`s academic studies can be accessed on his ResearchGate profile.